Матрицы

Определение матрицы

Матрица – это двумерный массив значений упорядоченных в строки и столбцы. Матрицу обычно записывают в квадратных или круглых скобках и разделяют элементы запятыми или пробелами. Например, матрица 2x2:

Здесь \(a, b, c, d\) – это элементы матрицы. Эта матрица имеет две строки и два столбца.

В общем случае, форму матрицы обзначают \(m \times n\), где \(m\) – количество строк, \(n\) – количество столбцов.

\(3 \times 2\):

\(2 \times 3\):

Когда одна из размерностей матрицы равна единице она называется вектором. Если размерность \(m \times 1\), то такой вектор называется вектор-столбец, например:

Если размерность \(1 \times n\), то такой вектор называется вектор-строка, например:

В общем случае матрица \(m \times n\):

Матрица со случайными элементами, равномерно распределенными на интервале (0, 1) размерностью \(2 \times 3\) в Matlab >> rand(2, 3):

ans =
    0.8147    0.1270    0.6324
    0.9058    0.9134    0.0975

Сложение и умножение матриц

Сложение матриц:

Числовой пример:

Matlab: >> [1 2; 3 4] + [5 6; 7 8]

Умножение матрицы на скаляр:

В Matlab: >> 3 * [1 1; 1 1]

Умножение двух матриц:

Для того чтобы две матрицы можно было умножить, количество столбцов первой матрицы должно совпадать с количеством строк второй матрицы.

Пусть \(A\) – матрица размера \(m \times n\) (\(m\) строк и \(n\) столбцов), а \(B\) – матрица размера \(n \times p\). Их произведение будет матрицей \(C\) размера \(m \times p\).

Элемент \(c_{ij}\) матрицы \(C\) вычисляется как скалярное произведение \(i\)-й строки матрицы \(A\) на \(j\)-й столбец матрицы \(B\). Формула для \(c_{ij}\) такова:

Т.е. каждый элемент \(c_{ij}\) матрицы \(C\) равен сумме произведений соответствующих элементов \(i\)-й строки матрицы \(A\) и \(j\)-го столбца матрицы B.

Например:

Следует иметь в виду, что операция перемножения матриц не коммутативна (\(AB \ne BA\) в общем случае):

Из \(AB=AC\) не следует, что \(B=C\):

Пусть:

A = [1 2; 2 4]; B = [2 1; 1 3]; C = [4 3; 0 2];
isequal(A*B, A*C)

ans = 1

isequal(A, C)

ans = 0

Умножение матриц разных размерностей:

A*B

ans =
    74    80    86    92
   173   188   203   218

shape = size(ans)

shape =
   2   4

ans * C

ans =
    7364    7696
   17354   18136

shape = size(ans)

shape =
   2   2

Умножение матриц ассоциативно:

, здесь \(A\), \(B\) и \(C\) – таких размеров, что данные произведения определены (т.е. \(A: m \times n, \space B: n \times p, \space C: p \times q\)).

Используя раннее определенные матрицы:

isequal((A*B)*C, A*(B*C))

ans = 1

Необходимость помнить о погрешностях вычисления:

Предположим, что мы хотим проверить ассоциативность умножения на случайно сгенерированных матрицах подходящих размерностей. Задав состояние (seed) случайного генератора (для того чтобы точно такой-же результат можно было повторить позже) для Matlab: rng(1), для Octave: rand('seed', 1) (стоит иметь в виду, что одинаковый seed не приведет к одинаковым результатам в разных языках), сгенерируем матрицы \(A: 2 \times 3, \space B: 3 \times 4,\space C: 4 \times 5\) заполненные случайными числами из равномерного распределения (\(0, 1\)):

A = rand(2, 3); B = rand(3, 4); C = rand(4, 5);
isequal((A*B)*C, A*(B*C))

ans =
   0

→ Неожиданный результат!

Проведем поэлементное сравнение:

(A*B)*C == A*(B*C)

ans =

   1   0   0   1   0
   0   0   0   1   1

В значительном количестве элементов матрицы не строго равны. Хотя на первый взгляд:

(A*B)*C 

ans =
    0.5053    0.6697    0.3570    0.4288    0.5599
    1.1254    1.4416    0.6967    1.0206    1.2094

A*(B*C)

ans =
    0.5053    0.6697    0.3570    0.4288    0.5599
    1.1254    1.4416    0.6967    1.0206    1.2094

Точность проведения различных операций значительно выше точности вывода по умолчанию.

Специальные матрицы

Нулевая матрица

Нулевая матрица — это матрица, все элементы которой равны нулю. Обозначается часто как \(O\) или \(0\), хотя это может вызывать путаницу с нулевым скаляром. Размеры нулевой матрицы могут быть любыми, например, \(m \times n\), где \(m\) – количество строк, а \(n\) – количество столбцов.

Примеры нулевых матриц:

В Matlab: >> zeros(2, 2)

В Matlab: >> zeros(3, 2)

Нулевая матрица обладает рядом свойств:

1. При сложении с любой другой матрицей того же размера результатом будет эта другая матрица;
2. При умножении на нулевую матрицу результатом всегда будет нулевая матрица (при условии, что умножение матриц определено).

Часто нулевая матрица использется в контексте задания СЛАУ (Системы Линейных Алгебраических Уравнений) в матричной форме:

, где:

• \(A\) – матрица коэффициентов рамзерностью: \(m \times n\);
• \(x\) – вектор-столбец размерностью \(n \times 1\);
• \(0\) – нулевой вектор-столбец размерностью \(m \times 1\).

Единичная матрица:

Единичная матрица – это квадратная матрица, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю. Обозначается обычно как \(I\) или \(I_n\), где \(n\) – размер матрицы (количество строк или столбцов, поскольку матрица квадратная).

Например, единичная матрица \(I_2\) размера \(2 \times 2\) выглядит следующим образом:

В Matlab: >> eye(2)

Единичная матрица \(I_3\) размера \(3 \times 3\):

В Matlab: >> eye(3)

Единичная матрица обладает рядом свойств:

1. При умножении единичной матрицы на любую другую матрицу подходящего размера результатом будет эта другая матрица: \(IA = A\) и \(AI = A\), т.е. единичная матрица является нейтральным элементом операции умножения матриц;
2. Обратная матрица к единичной матрице является единичной матрицей;

В Matlab функция eye(2, 3) создаст матрицу размером \(2 \times 3\), в которой на главной диагонали стоят единицы, а все остальные элементы равны нулю. Обратим внимание, что полученная матрица не является квадратной; у неё 2 строки и 3 столбца. Строго говоря это не единичная матрица, которая должна быть квадратной, но принцип похож: единицы на главной диагонали.

Вот как будет выглядеть результат:

Функция eye(n, m) в общем случае создаёт матрицу размером \(n \times m\) с единицами на главной диагонали и нулями во всех остальных позициях.

Диагональная матрица

Диагональная матрица – это квадратная матрица, в которой все элементы, не лежащие на главной диагонали, равны нулю. Элементы на главной диагонали могут быть как нулевыми, так и ненулевыми.

Единичная матрица \(D_3\) размера \(3 \times 3\):

В Matlab:

diag([1 2 3])

ans =

   1   0   0
   0   2   0
   0   0   3

В Matlab:

diag([1 2 3; 4 5 6; 7 8 9])

ans =
     1
     5
     9

Верхнетреуголная матрица

Верхнетреугольная матрица – это квадратная матрица, у которой все элементы ниже главной диагонали равны нулю. Элементы на главной диагонали и выше не ограничены и могут принимать любые значения, включая ноль.

Верхнетреуголная матрица размера \(3 \times 3\):

В Matlab:

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
U = triu(A)

U =
   1   2   3
   0   5   6
   0   0   9

Верхнетреуголная единичная:

U = triu(ones(3,3));

U =
   1   1   1
   0   1   1
   0   0   1

Нижнетреуголная матрица

Нижнетреугольная матрица – это квадратная матрица, у которой все элементы выше главной диагонали равны нулю. Элементы на главной диагонали и ниже не ограничены и могут принимать любые значения, включая ноль.

Нижнетреугольная матрица размера \(3 \times 3\):

В Matlab:

A = [1, 2, 3; 4, 5, 6; 7, 8, 9];
L = tril(A)

L =
     1     0     0
     4     5     0
     7     8     9

Транспонирование матрицы

Транспонирование матрицы – это операция, при которой строки исходной матрицы преобразуются в столбцы, а столбцы – в строки. Другими словами, элементы матрицы отражаются относительно её главной диагонали.

Пусть дана матрица \(A\) размером \(m \times n\). Транспонированная матрица \(A^T\) будет иметь размер \(n \times m\) и определяется следующим образом: \(\forall i,j: A^T_{ij} = A_{ji}\).

В качестве примера рассмотрим матрицу:

Результатом транспонирования матрицы \(A\), будет:

В Matlab:

A = [1 2 3; 4 5 6];
A'

ans =
     1     4
     2     5
     3     6

Свойства транспонирования матрицы:

1. \((A^{T})^{T} = A\);
2. \((\lambda \cdot A)^T = \lambda \cdot A^{T}\);
3. \((A + B)^T = A^T + B^T\);
4. \((A \cdot B)^T = B^T \cdot A^T\);

Симметричная матрица

Симметричная матрица — это квадратная матрица, которая равна своей транспонированной матрице \(A = A^T\). Элементы симметричной матрицы симметричны относительно главной диагонали.

Пример симметричной матрицы:

Проверка на симметрию в Matlab: >> isequal(A, A')

Кососимметричная матрица

Кососимметричная (или антисимметричная) матрица — это квадратная матрица, которая удовлетворяет условию \(A = -A^T\). Другими словами, транспонированная матрица является аддитивным обратным к исходной матрице. Это также означает, что все элементы на главной диагонали кососимметричной матрицы равны нулю.

Кососимметричная матрица \(3 \times 3\):

Проверка на кососимметрию в Matlab: >> isequal(A, -A')

Скалярное, векторное и тензерное произведение векторов

Скалярное произведение (иногда называемое внутренним произведением) двух векторов \(\overline{a}\) и \(\overline{b}\) – это сумма произведений соответствующих компонент этих векторов. Если имеются два вектора \(\overline{a} = (a_1, a_2, \ldots, a_n)\), \(\overline{b} = (b_1, b_2, \ldots, b_n)\), тогда:

Частые обозначения скалярного произведения: \(\overline{a} \cdot \overline{b}\), \(\langle \overline{a}, \overline{b} \rangle\), \((\overline{a}, \overline{b})\).

Геометрически:

– произведение длин на косинус угла между ними.

Если \(\langle \overline{a}, \overline{b} \rangle = 0\), то \(\overline{a}\) и \(\overline{b}\) – ортогональны.

В контексте матричной алгебры скалярное произведение представляется как произведение вектора-строки на вектор-столбец, учитывая, что при создании векторов в Matlab по умолчанию создаются вектора-строки, тогда:

a = [1 2 3]; b = [4 5 6];
a*b'

ans = 32

Также можно использовать специальную функцию:

dot(a, b)

ans = 32

Векторное произведение – это операция над двумя векторами в трехмерном пространстве, результатом которой является новый вектор. Этот новый вектор перпендикулярен плоскости, определяемой исходными векторами, а его длина равна площади параллелограмма, образованного этими векторами.

Если \(\overline{a} = (a_1, a_2, a_3)\), \(\overline{b} = (b_1, b_2, b_3)\) – два вектора в трехмерном пространстве, их векторное произведение \(\overline{a} \times \overline{b}\) определяется следующим образом:

Частые обозначения векторного произведения: \(A \times B\), \([A, B]\)

Для вычисления вектороного произведения в Matlab испольузется следующая фукнция:

a = [1 2 3]; b = [4 5 6];
cross(a, b)

ans =
  -3   6  -3

Тензорное произведение двух векторов – это способ комбинирования двух векторов так, чтобы получить новый математический объект, который сохраняет некоторую информацию о структуре каждого из исходных векторов. В контексте евклидовых векторов результатом тензорного произведения двух векторов \(\overline{a}\) и \(\overline{b}\) является матрица, элементы которой равны произведениям соответствующих элементов исходных векторов.

Пусть \(\overline{a}= (a_1, a_2, \ldots, a_n)\) и \(\overline{b} = (b_1, b_2, \ldots, b_m)\). Тогда тензорное произведение \(\overline{a} \otimes \overline{b}\) будет матрицей размера \(n \times m\) с элементами \(a_i \cdot b_j\):

В контексте матричной алгебры тензерное произведение двух векторов представляется как произведение вектора-столбца на вектор-строки.

Пусть:

Тогда:

В Matlab по умолчанию создаются вектора-строки, поэтому тензерное произведение получается путем транспонирования первого, а не второго вектора \(u \otimes v = u^T \cdot v\). Например:

a = [1 2 3]; b = [4 5 6];
a'*b

ans =
    4    5    6
    8   10   12
   12   15   18

Что то же самое, что:

A = [a' a' a'];
B = [b; b; b];
A .* B

ans =
    4    5    6
    8   10   12
   12   15   18

Обратная матрица

Обратная матрица – это квадратная матрица \(A^{-1}\), которая при умножении на исходную матрицу \(A\) даёт единичную матрицу того же порядка \(I\).

Некоторые свойства обратной матрицы:

• Единственность: Для любой невырожденной (определитель которой не равен нулю) квадратной матрицы существует только одна обратная матрица.
• Существование обратной матрицы: Матрица имеет обратную тогда и только тогда, когда ее определитель не равен нулю. Если определитель равен нулю, матрица называется вырожденной, и у нее нет обратной матрицы.
• Обратная матрица произведения: Если \(A\) и \(B\) — квадратные невырожденные матрицы одного и того же порядка, то: \((AB)^{-1}=B^{-1}A^{-1}\)
• Транспонирование: Если \(A\) имеет обратную матрицу, то обратная для транспонированной матрицы \(A^T\) будет равна транспонированной матрице от \(A^-1\): \((A^T)^{-1} = (A^{-1})^T\)
• Умножение на скаляр: Если \(A\) и \(B\) — обратимые матрицы (имеют обратные), и \(c\) - скаляр, то: \((cA)^{-1} = \frac{1}{c} A^{-1}\) (где \(c\) не равно нулю)
• Обратная матрица суммы: В общем случае, сумма обратных матриц не равна обратной матрице суммы, т.е.: \((A + B)^{-1} \neq A^{-1} + B^{-1}\).

Рассмотрим пример нахождения обратной матрицы для \(A_{2 \times 2}\):

, здесь вторая матрица – обратная матрица, которую необходимо найти.

Представим матричное умножение в виде системы уравнений:

Имеются 4 уравнения и 4 неизвестных → постараемся найти решение системы.

Выражая из однородных уравнений¹ \(y_1\) и \(y_2\), а затем подставляя в первое и четвертое получим решение:

В иной форме:

Заметим, что решение существует тогда, когда \(ad - bc \ne 0\), что является определителем матрицы \(A_{2 \times 2}\).

В общем случае обратную матрицу можно определить как:

\(A^{-1} = \frac{\text{adj} A}{|A|}\) , где \(\text{adj} A\) – соответсвующая присоединенная матрица, \(|A|\) – определитель матрицы \(A\).

Из этого определения следует критерий обратимости: матрица обратима тогда и только тогда, когда она невырождена, то есть её определитель не равен нулю. Для неквадратных матриц и вырожденных матриц обратных матриц не существует.

В Matlab:

A = [1 2, 3 4];
B = inv(A)

Теперь, матрица \(B\) будет содержать обратную матрицу для \(A\):

B =
  -2.0000   1.0000
   1.5000  -0.5000

Однако стоит быть осторожным при использовании inv(). В некоторых случаях, особенно когда матрица \(A\) близка к вырожденной, использование inv(A) может привести к численным неточностям. Во многих приложениях, вместо явного вычисления обратной матрицы, лучше решать систему уравнений напрямую с помощью оператора \.

Пример. Решите систему линейных уравнений:

A = [3, 4, 5; 2, -3, 7; 1 -6 1]
B = [2; -1; 3]
X = A \ B
A * X

A =
     3     4     5
     2    -3     7
     1    -6     1

B =
     2
    -1
     3

X =
    2.6196
   -0.2283
   -0.9891

ans =
    2.0000
   -1.0000
    3.0000

Ортогональная матрица

Ортогональная матрица — это квадратная матрица \(Q\), которая удовлетворяет условию:

где \(Q^T\) — это транспонированная матрица \(Q\), а \(I\) — это единичная матрица того же порядка, что и \(Q\).

Иначе говоря, столбцы ортогональной матрицы образуют ортонормированный базис в евклидовом пространстве: все столбцы имеют длину 1 и они попарно ортогональны друг другу.

Одно из полезных свойств ортогональных матриц заключается в том, что их обратная матрица совпадает с транспонированной матрицей, т.е. \(A^{-1} = A^T\).

Ещё одно важное свойство ортогнальной матрицы – это то, что она сохраняет длину. Предположим, что имеется вектор \(v\) в некотором евклидовом пространстве. Если умножите этот вектор на ортогональную матрицу \(A\), то получившийся вектор \(Av\) будет иметь ту же длину, что и исходный вектор \(v\). Т.е. ортогональная матрица позволяет проводить преобразование без искажения длин векторов:

Получение ортогональной матрицы в Matlab:

Имея матрицу можно воспользоваться функцией qr проводящую QR - факторизацию (разложение матрицы на ортогональную и верхнетреугольную).

A = randn(3,3); % 3x3 random matrix
[Q, R] = qr(A); % QR decomposition

В этом примере Q – \(3 \times 3\) ортогональная матрица.

Проверка на ортогональность матрицы в Matlab:

Можно проверить, является ли матрица ортогональной, проверив, совпадает ли её транспонированная матрица с её обратной матрицей.

is_orthogonal = norm(Q'*Q - eye(3)) < 1e-10;

Здесь рассчитывается фробениусова (евклидова) норма разницы \(Q^TQ - I\). Если эта норма очень близка к нулю (меньше некоторой маленькой погрешности, скажем, \(1^{-10}\), то пологаем, что матрица является ортогональной.

Определитель ортогональной матрицы равен \(-1\) или \(1\), если \(Q\) - ортогональная матрица, тогда >> det(Q) \(\sim\) -1 или 1.

Матрица вращения

Примером ортогональной матрицы служит матрица вращения.

Матрица вращения (матрица поворота) - это матрица, используемая для для выполнения вращения на заданный угол и в заданном направлении. В частности, для 2D и 3D пространств матрицы вращения часто используются в компьютерной графике (например компьютерных играх) и систем управления (например робототехнике).

Матрица поворота, исходя из правил матричной алгебры, может трансформировать как вектор, так и матрицу.

Рассмотрим сначала задачу поворота вектора. Представим, что над гладью воды зависла удочка рыбака под углом \(\phi = 45^{\circ}\). Вдруг - поклёв! Рыбак потянул удочку, и она стала быстро набирать высоту, длина лески (катет А) стала расти, а расстояние от рыбака до самой лески стало уменьшаться (катет B). Длина самой удочки совсем не изменилась, даже когда она описала в воздухе дугу и оказалась почти над головой рыбака, под углом \(\phi = 90^{\circ}\). Длина лески сравнялась с длиной удочки, а расстояние между рыбаком и леской изменилось до 0, леска оказалась в руках рыбака.

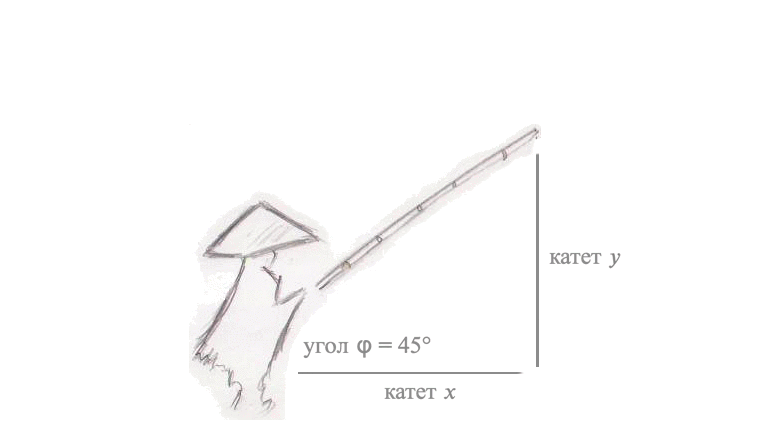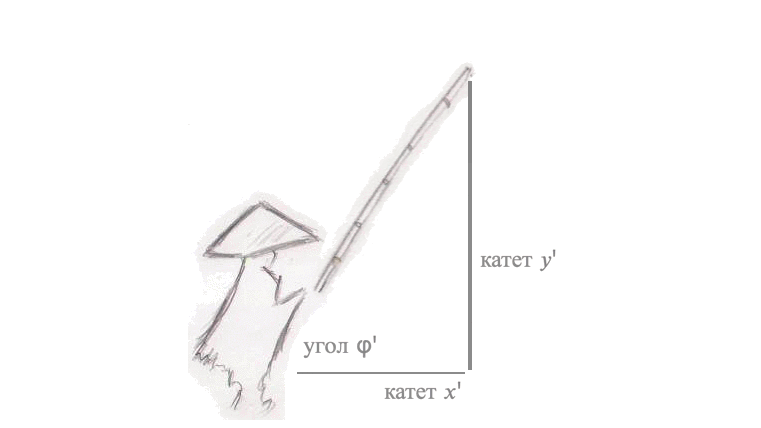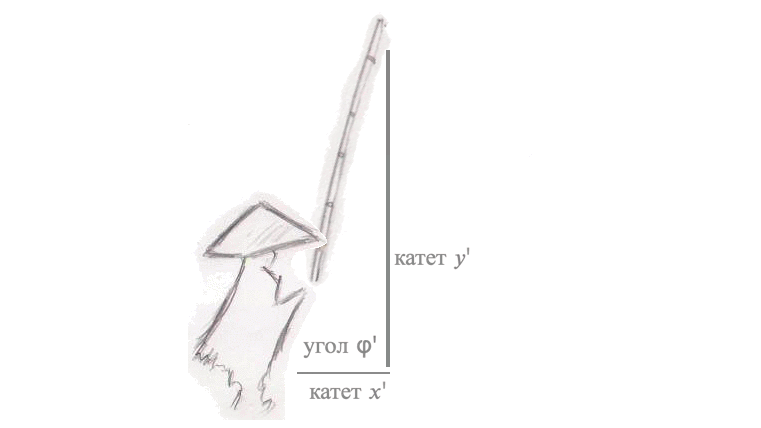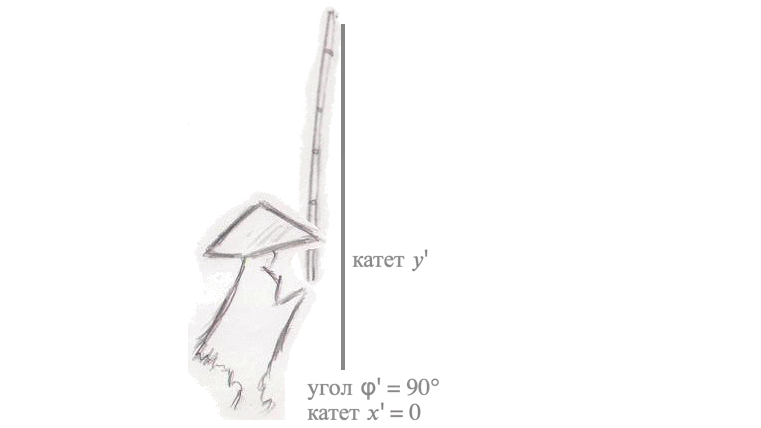
Пусть: длина удочки – \(r\), длина лески – \(y\), а \(x\) - расстояние между рыбаком и тем местом, где леска погружена в воду. Тогда, вспоминая теорему Пифагора: \(r^2 = y^2 + x^2\).

• Отношение длины лески к длине удочки – \(\sin \phi\)
• Отношение длины отрезка между рыбаком и местом погружения лески с длиной удочки — \(\cos \phi\)

→

Пусть вектор-удочка - это радиус вектор, тогда его начальный координаты \((x, y)\), а координаты после поворота \((x', y')\). Измененный угол наклона к глади воды: \(\phi' = \phi + \theta\), где \(\theta\) угол поворота.

Так как длина удочки не меняется \(r\) можно выразить через новые углы и катеты:

Домножив результат на \(r\):

Учитывая, что \(r^2 = x'^2 + y'^2\):

Принимая тригонометрические функции от угла поворота за коэффициенты, можно представить новые координаты как результат перемножения на матрицу вращения \(R_{\theta}\):

Тогда для того чтобы получить новые координаты вектора имея старые и угол вращения:

Матрица от обратного угла \(R_{-\theta}\), равна обратной матрицы \(R_{\theta}^{-1}\), а так как матрица ортогональна, то:

Поворот на \(\frac{\pi}{4}\) в Matlab:

theta = pi/4; % Example: 45-degree rotation in radians
R2D = [cos(theta), -sin(theta); sin(theta), cos(theta)];
v = [1; 0]; % Example 2D vector
v_rotated = R2D * v

v_rotated =
    0.7071
    0.7071

Итерирование по матрице с помощью цикла

Пример 1. Обработка двумерных массивов производится с помощью двух вложенных циклов. Например, посчитать сумму всех элементов можно следующим образом.

A = [
  1 2 3 4,
  5 6 7 8,
  9 10 11 12
];
[n, m] = size(A);
s = 0;
for i = 1:n
    for j = 1:m
        s = s + A(i, j);
    end
end
s

78

sum(sum(A))

Пример 2. Выведем элементы стоящие на главной диагонали квадратной матрицы

A = [
  0 1 1 1 1
  2 0 1 1 1
  2 2 0 1 1
  2 2 2 0 1
  2 2 2 2 0
];
for i = 1:size(A, 1)
    fprintf('%d ', A(i, i));
end 

0 0 0 0 0 

diag(A)

ans =
     0
     0
     0
     0
     0

Пример 3. Выведем элементы верхнего треугольника:

for i = 1:size(A, 1)-1
    for j = i+1:size(A, 1)
      fprintf('%d ', A(i, j));
    end
    fprintf('\n');
end 

1 1 1 1 
1 1 1 
1 1 
1 

triu(A)

ans =
     0     1     1     1     1
     0     0     1     1     1
     0     0     0     1     1
     0     0     0     0     1
     0     0     0     0     0

Пример 4. Выведем элементы нижнего треугольника:

for i = 2:size(A, 1)
    for j = 1:i-1
      fprintf('%d ', A(i, j));
    end
    fprintf('\n');
end 

2 
2 2 
2 2 2 
2 2 2 2 

tril(A)

ans =
     0     0     0     0     0
     2     0     0     0     0
     2     2     0     0     0
     2     2     2     0     0
     2     2     2     2     0