Первое знакомство с Big 0
О большое (англ. Big O) - математическое обозначение для сравнения асимптотического поведения функции.
– Википедия
Концепция Big O необходима для описания эффективности алгоритмов. Ни один серьезный проект и ни одно серьезное собеседование не может обойтись без вопросов о Big O, ведь она необходима для выявления и исправления неоптимального кода.
Эффективность алгоритмов описывается с помощью двух характеристик: времени и памяти. Здесь речь пойдет именно о первой составляющей.
Эффективный с точки зрения времени алгоритм — это быстрый алгоритм. Но что считается быстрым? Небольшой массив может обрабатываться за 10 секунд, а больший — за 100 секунд. Интуитивно понятно, что время выполнения зависит от размера массива и характеристик ЭВМ.
Решение заключается в оценке верхней границы временной сложности как количества операций, необходимых для выполнения алгоритма в зависимости от входных данных. Это позволяет оценить, насколько хорошо алгоритм масштабируется с увеличением объема данных.
Для упрощения расчетов часто игнорируют разницу в скорости выполнения различных операций. Например, деление чисел с плавающей точкой и сложение целых чисел в теории алгоритмов считаются равнозначными по сложности, несмотря на различия в затратах процессорного времени. При оценке верхней границы внимание сосредотачивается на наиболее значимых аспектах алгоритма.
Рассмотрим аналогию из жизни. Вы собираетесь завтра полететь к другу в гости на киномарафон. У вас есть загруженная кинобиблиотека. Если планируется посмотреть небольшое количество фильмов, то вероятно будет быстрее отправить файлы по сети; в противном случае лучше взять с собой носитель с фильмами.
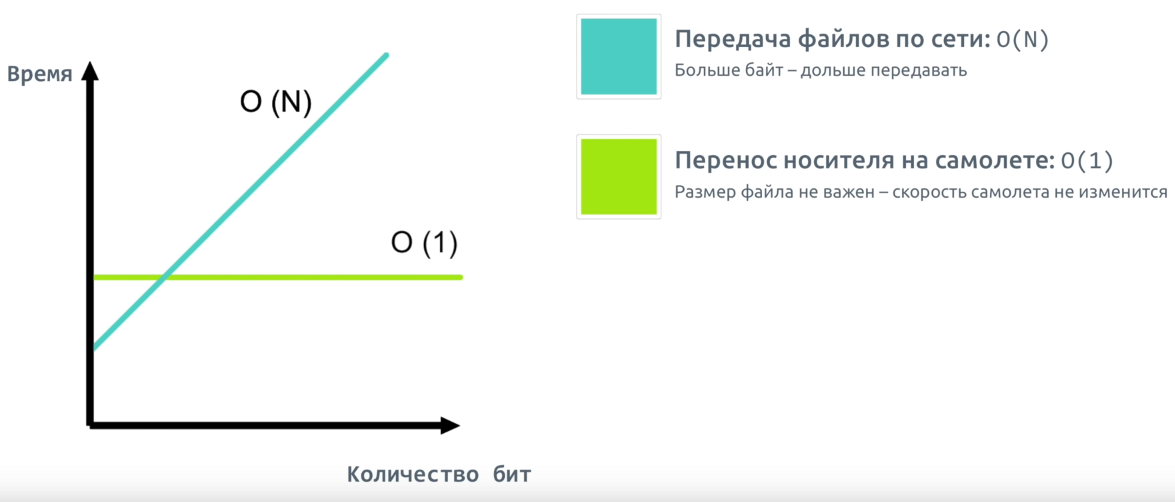
В первом случае сложность является константной: независимо от количества фильмов на носителе, вашему другу придется ждать вашего прилета. Во втором случае время передачи прямо пропорционально количеству передаваемых бит, зависимость — линейная.
Сложность O(1) и O(n)
O(1) обозначает константную сложность. Время выполнения не зависит от размера входных данных.
Возьмем массив из 5 чисел:
nums = [1, 3, 7, 5, 9];Допустим, нам необходимо получить третий элемент:
nums(3) % выводит 7Операция извлечения не зависит от размера массива, потому что, зная индекс элемента, мы знаем его адрес в памяти. Время такой операции не зависит от количества элементов, хранящихся в памяти.
Алгоритмы со сложностью O(1) являются наиболее эффективными.
O(n) обозначает линейную сложность. Время выполнения алгоритма линейно зависит от размера входных данных.
Рассмотрим пример нахождения суммы элементов массива.
nums = [1, 2, 3, 4, 5];
s = 0;
for s = nums
s = s + num;
endВ этом случае нам необходимо перебрать все элементы массива. Количество операций прямо пропорционально количеству элементов.
Пример рекурсивной реализации:
function s = sumRecursive(n)
if n == 1
s = 1;
else
s = n + sumRecursive(n - 1);
end
endУ этой функции сложность тоже \(O(n)\).
Что насчет следующей функции?
function sum = pairSumSequence(n)
sum = 0;
for i = 0:n-1
sum = sum + pairSum(i, i+1);
end
end
function result = pairSum(a, b)
result = a + b;
endСложность функции pairSumSequence зависит от сложности функции pairSum. Функция pairSum выполняет сложение a + b и не содержит циклов или рекурсии, она всегда выполняет константное количество операций, следовательно, сложность функции pairSum — \(O(1)\). В функции pairSumSequence в цикле выполняется pairSum, и он выполняется от \(0\) до \(n-1\). Таким образом, сложность pairSumSequence также \(O(n)\).
Можем ли мы сделать суммирование более эффективным? В общем случае нет. А если мы знаем, что массив начинается с единицы, отсортирован и каждый последующий элемент всегда больше предыдущего на единицу? Тогда мы можем воспользоваться формулой: \(S = \frac{n(n+1)}{2}\).
function sum_ary = sumContiguousArray(ary)
% Get the last item
last_item = ary(end);
% Gauss's trick
sum_ary = last_item * (last_item + 1) / 2;
end
nums = [1, 2, 3, 4, 5];
sum_ary = sumContiguousArray(nums)sum_ary =
15
Такой алгоритм гораздо эффективнее \(O(n)\), более того, он выполняется за «постоянное/константное время», т.е. это \(O(1)\).
Отбрасывание констант в оценках Big O связано с тем, что это асимптотическая оценка: мы рассматриваем поведение алгоритма при стремлении размера входных данных к бесконечности.
Если алгоритм выполняет для \(n\) элементов \(n\) шагов, и еще один шаг для вывода информации, мы все равно говорим, что его сложность — \(O(n)\). В контексте асимптотики, бесконечность значительно превышает любую константу.
Например, \(O(2n) = O(n)\), \(O(3n) = O(n)\), \(O(5n) = O(n)\). Две бесконечности, три бесконечности и пять бесконечностей по сути одно и то же. Также упрощаются выражения \(O(2) = O(1)\), \(O(3) = O(1)\), \(O(5) = O(1)\).
Big O дает асимптотическую оценку, фокусируясь только на скорости роста сложности при бесконечном увеличении входных данных.
Рассмотрим примеры:
ary = [1, 7, 2, 3, 6];
min_val = inf;
max_val = -inf;
for x = ary
if x < min_val
min_val = x;
end
if x > max_val
max_val = x;
end
endСложность алгоритма \(O(n)\).
ary = [1, 7, 2, 3, 6];
min_val = inf;
max_val = -inf;
for x = ary
if x < min_val
min_val = x;
end
end
for x = ary
if x > max_val
max_val = x;
end
endСложность алгоритма \(O(2n) = O(n)\).
Неважная сложность — это еще одно важное понятие при проведении асимптотической оценки. Она отвечает на вопрос о том, как обращаться со сложностью вида \(O(n^2 + n)\), где \(n\) — не константа. Поскольку мы оцениваем верхнюю границу, можно заменить \(O(n^2 + n)\) на \(O(n^2 + n^2)\), так как \(n^2\) значительно больше \(n\). В результате получаем \(O(n^2 + n^2) = O(2n^2) = O(n^2)\).
Несколько примеров:
- \(O(N + \log N) = O(N)\);
- \(O(5 \cdot 2^N + 10 \cdot N^{100}) = O(2^N)\);
- \(O(N^2 + B) = O(N^2 + B)\).
В последнем выражении упрощение невозможно, пока мы не знаем конкретные значения \(B\).
Складывать или умножать сложности выполнения?
Рассмотрим следующий пример:
for a = arrA
disp(a);
end
for b = arrB
disp(b);
end
Наш код сначала проходит по массиву длиной \(A\), затем — по массиву длиной \(B\). Сложность данного алгоритма равна \(O(A + B)\), так как проходы по массивам производятся последовательно, и выполнение первого цикла не зависит от второго.
for a = arrA
for b = arrB
disp([num2str(a) ',' num2str(b)]);
end
end
Для каждого элемента a выполняется проход по всем элементам массива b. Циклы вложены и зависят друг от друга, так как один из них выполняется в теле другого. Сложность такой конструкции составляет \(O(A \times B)\).
Не самые лучшие решения: O(n^2)
Рассмотрим следующий алгоритм, который проверяет массив на наличие дубликатов:
function has_duplicates = checkForDuplicates(nums)
num_elements = length(nums);
has_duplicates = false;
for i = 1:num_elements
current_num = nums(i);
for j = 1:num_elements
if j == i
continue;
end
if nums(j) == current_num
has_duplicates = true;
break;
end
end
if has_duplicates
break;
end
end
end
nums = [1, 2, 3, 4, 5, 5];
result = checkForDuplicates(nums); % returns true
disp(result);
Итерирование по массиву имеет сложность O(n). В данном алгоритме используется вложенный цикл, так что для каждого элемента происходит повторное итерирование по массиву — это создаёт сложность O(n^2), или «сложность порядка n квадрат».
Хотя в алгоритме выше не всегда будут перебраны все элементы, при оценке сложности по методике Big O обычно рассматривается худший случай.
«Сложность порядка log n»: O(log n)
Вложенный цикл в алгоритме можно использовать для поиска элемента в массиве. При определённых условиях, такой поиск можно оптимизировать, сделав его быстрее, чем линейный поиск O(n).
Предположим, что массив отсортирован. Тогда мы можем использовать алгоритм «бинарного поиска»:
- Берём середину массива.
- Если искомое число меньше значения в середине, идём в левый подмассив. Если больше — в правый.
- Повторяем ту же процедуру для выбранного подмассива.
- Прекращаем поиск, когда найдём элемент или когда длина подмассива станет равной 1.
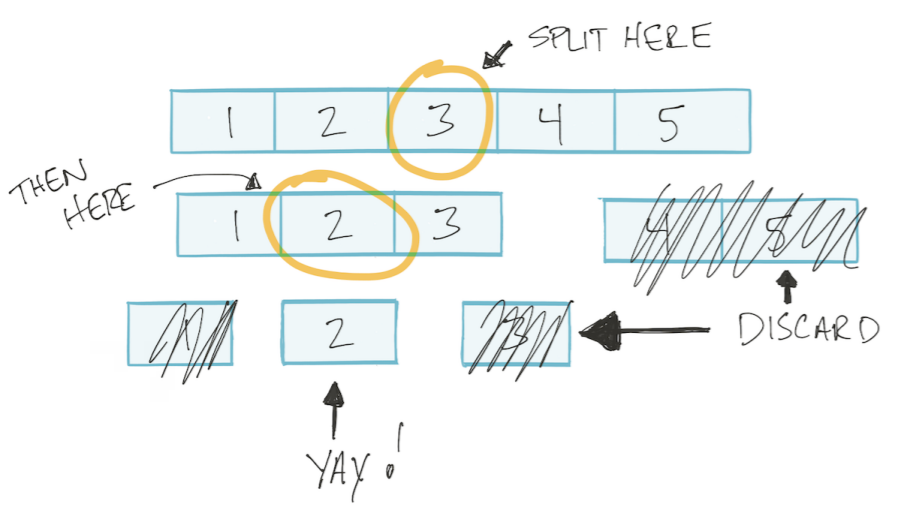
Для массива длиной \(N = 16\):
- \(N = 16\) разделили на 2,
- \(N = 8\) разделили на 2,
- \(N = 4\) разделили на 2,
- \(N = 2\) разделили на 2,
- \(N = 1\).
4 — это максимальное количество операций, которое необходимо выполнить алгоритму, чтобы найти ответ. Запишем зависимость в виде: \(2^4 = 16\).
В общем виде: \(2^k = N\). \(k = \log_2 N\). Так как значение \(k\) является Big O, то \(O(k) = O(\log_2 N)\). Основание логарифма не играет роли (так как является константой), поэтому: \(O(k) = O(\log N)\).
Вывод: для алгоритма, где на каждой итерации выбирается половина элементов, сложность будет \(O(\log N)\).
Алгоритм бинарного поиска:
function result = binarySearch(arr, x)
low = 1;
high = length(arr);
while low <= high
mid = low + floor((high - low) / 2);
% Проверяем, присутствует ли x в середине
if arr(mid) == x
result = mid;
return;
% Если x больше, игнорируем левую половину
elseif arr(mid) < x
low = mid + 1;
% Если x меньше, игнорируем правую половину
else
high = mid - 1;
end
end
% Если мы достигли этой точки, элемент не найден
result = -1;
end
nums = [1, 2, 3, 4, 5];
binarySearch(nums, 2)ans =
2
Улучшим O(n^2) до O(n log n)? Или нет?
Вернемся к задаче проверки массива на наличие дубликатов. Исходный метод перебирает все элементы массива, и для каждого элемента снова производит перебор. Это дает сложность \(O(n \times n)\) или \(O(n^2)\).
Мы можем рассмотреть возможность использования бинарного поиска вместо второго перебора. Таким образом, сохраняя перебор всех элементов \(O(n)\), внутри каждой итерации мы бы выполняли бинарный поиск \(O(\log n)\), что приводит к общей сложности \(O(n \log n)\).
function has_duplicates = checkForDuplicates(nums)
num_elements = length(nums);
has_duplicates = false;
for i = 1:num_elements
current_num = nums(i);
sub_nums = nums([1:i-1, i+1:end]);
has_duplicates = binarySearch(sub_nums, current_num) ~= -1;
if has_duplicates
break;
end
end
end
nums = [1, 2, 3, 4, 5, 5];
result = checkForDuplicates(nums); % trueОднако, чтобы бинарный поиск был эффективен, массив должен быть отсортирован, что само по себе требует времени \(O(n \log n)\).
Если массив уже отсортирован, поиск дубликатов может быть выполнен за \(O(n)\) путем линейного прохода и сравнения каждого элемента с его соседом. Этот метод гораздо эффективнее и проще, чем использование бинарного поиска в данной задаче.